Теоремата за невъзможността на Arrow гласи, че ясните предпочитания, класирани в общността, не могат да бъдат определени чрез преобразуване на предпочитанията на индивидите от справедлива избирателна система с гласувано класиране. Теоремата е изследване на социалния избор и е известна също като „Теоремата за общата възможност“ или „Парадоксът на Arrow“. Теоремата за невъзможността на Arrow е кръстена на икономиста Кенет Ароу, демонстрирана в статията му „Трудност в концепцията за социално благосъстояние“.

Обобщение
- Теоремата за невъзможността на Arrow гласи, че избирателната система с класирано гласуване не може да достигне предпочитания в общността, като преобразува предпочитанията на индивидите, като същевременно отговаря на всички условия на справедлива система за гласуване.
- Условията за разумно справедлива избирателна система включват недиктатура, неограничен домейн, независимост на неподходящи алтернативи, социална подредба и ефективност на Парето.
- Теоремата не обхваща избирателните системи с гласуване на кардинали.
Разбиране на теоремата за невъзможността на Arrow
Теоремата за невъзможността на Arrow е теория за социалния избор, която изучава комбинирането на предпочитания, благосъстоянието и мненията на индивидите, за да се стигне до социално благосъстояние или решения в общността. В него се обсъждат недостатъците на избирателната система с класирано гласуване.
Според теорията за невъзможността, когато има повече от два варианта, е невъзможно системата за гласуване с класиране да достигне общ ред на предпочитанията чрез събиране и преобразуване на заповедите за предпочитания на индивидите, като същевременно отговаря на набор от условия. Условията са изискванията за разумно справедлива процедура на гласуване и ще бъдат разгледани допълнително в следващия раздел.
За по-добро разбиране на теоремата, ето един пример, който обяснява защо заповедите за предпочитания на индивидите не могат да бъдат преобразувани в обществен ред. Да приемем, че има три алтернативи (опции) при гласуване с класиране: X, Y и Z. Следващата таблица показва резултатите от гласуването от 100 гласували:

Въз основа на резултатите, опция X ще спечели, тъй като редът X> Y> Z събира най-много гласове (45 избиратели предпочитат Y пред Z и предпочитат X пред Y). Редът с опция Z като най-предпочитано показва най-малък брой гласове, като само 20 избиратели предпочитат Z пред другите две алтернативи. Ако обаче опцията Y вече не е налична алтернатива, резултатът ще бъде обърнат.
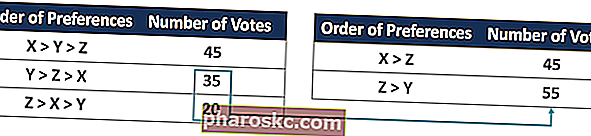
Общият брой гласове за Z над X ще бъде 55 (комбинирайки гласовете за поръчките Y> Z> X и Z> X> Y), а гласовете за X над Z все още са 45. Резултатът означава, че Z е социално класиран над X. Конфликтният резултат е доказателство за теоремата за невъзможността на Arrow.
Условия в теоремата за невъзможността на Arrow
Както бе споменато по-горе, има набор от условия (критерии) за разумно справедлива избирателна процедура. Той включва недиктатура, неограничен домейн, независимост на неподходящи алтернативи, социална подредба и ефективност на Парето.
1. Недиктатура
Недиктатурата означава, че един избирател и предпочитанията на избирателя не могат да представляват цяла общност. Функцията за социално подпомагане трябва да отчита желанията на множество избиратели.
2. Неограничен домейн
Неограничен домейн изисква да бъдат отчетени всички предпочитания на всеки избирател, което дава пълна класация на социалните предпочитания.
3. Независимост на неподходящи алтернативи (IIA)
Условието за независимост на неподходящите алтернативи изисква, когато класирането на индивидите на неподходящи алтернативи на подмножество се промени, социалното класиране на подмножеството не трябва да се влияе. Примерът, споменат в горния раздел, нарушава условието. За да се изпълни условието IIA, резултатът трябва да остане същият (опция X все още трябва да бъде социално класирана над опция Z), когато опцията Y бъде премахната.
4. Социално подреждане
Условието за социална подредба изисква избирателите да могат да подреждат избора си във връзка и преходна връзка, т.е. от по-добро към по-лошо.
5. Ефективност на Парето
За ефективността на Парето Ефективност на Парето Ефективността на Парето, често използвана в икономиката, е икономическа ситуация, при която е невъзможно да се направи една партия по-добра, без да се влоши друга партия. , трябва да се спазват единодушните предпочитания на отделните лица. Редът на социалните предпочитания трябва да се съгласува с този на индивидуалните предпочитания, ако всеки избирател стриктно предпочита една от алтернативите пред друга. Резултатът не трябва да е чувствителен към профила на предпочитанията.
Кардиналско гласуване срещу класирано гласуване
Теоремата за невъзможността на Arrow се прилага само за избирателна система с класирано гласуване, но не и за избирателна система с гласуване с кардинал. При класираното гласуване избирателите дават класирани бюлетини и класират избора си по ред. При кардинално гласуване избирателите дават оценени бюлетини и могат да оценят всеки избор независимо.
Цифрови оценки могат да се присвояват на опции при гласуване с кардинал. В сравнение с класираното гласуване, кардиналното гласуване предоставя повече информация, което прави възможно системата за гласуване на кардинали да преобразува заповедите за предпочитания на отделните лица в социален ред за предпочитания.
„Изходи“ от теоремата за невъзможността на Arrow
Правят се някои опити да се избяга от теоремата за невъзможността и да се изследват възможностите. Такива опити могат да бъдат класифицирани в две основни категории. Единият включва подходите, които превръщат всеки профил на предпочитания в алтернативно или социално предпочитание. Подходите се опитват да отслабят или премахнат едно или повече от условията за справедлива избирателна система. Един пример е гласуването по двойки, което ограничава броя на алтернативите до две.
Другата категория включва подходи, които изследват други правила. Пример е избирателната система с гласуване на кардинал, която предоставя повече информация. По този начин основната полезност се счита за по-надежден инструмент за показване на социалното благосъстояние.
Допълнителни ресурси
Finance предлага сертифициран банков и кредитен анализатор (CBCA) ™ Сертифициране на CBCA ™ Сертифицираният банков и кредитен анализатор (CBCA) ™ е глобален стандарт за кредитни анализатори, който обхваща финанси, счетоводство, кредитен анализ, анализ на паричните потоци, моделиране на договори, заем изплащания и др. програма за сертифициране за тези, които искат да издигнат кариерата си на следващото ниво. За да продължите да учите и развивате своята база знания, моля, проучете допълнителните съответни ресурси по-долу:
- Groupthink Groupthink Groupthink е термин, разработен от социалния психолог Ървинг Янис през 1972 г., за да опише грешни решения, взети от група поради групов натиск. Груповото мислене е явление, при което начините за подхождане към проблемите или въпросите се разглеждат с консенсус на група, а не от лица, действащи независимо.
- Невидима ръка Невидима ръка Понятието "невидима ръка" е измислено от шотландския мислител на Просвещението Адам Смит. Той се отнася до невидимата пазарна сила, която довежда свободния пазар до равновесие с нивата на търсене и предлагане чрез действия на лични личности.
- Дилема на затворника Дилема на затворника Дилемата на затворника е парадокс на вземането на решения и теорията на игрите, илюстриращ, че двама рационални индивиди, вземащи решения в собствения си интерес
- Игра с нулева сума Сума с нулева сума (и без нулева сума) Играта с нулева сума е ситуация, при която загубите, направени от играч в транзакция, водят до еднакво увеличение на печалбите на противния играч. Той е кръстен по този начин, тъй като нетният ефект след печалби и загуби от двете страни е равен на нула.
